Finding the Rule or nth Terms of Quadratic Sequences
An example of a quadratic sequence is: 2, 4, 8, 14, 22
When we find the difference line we obtain
The difference line is not constant so it cannot be an arithmetic sequence. However we can construct a second difference line – the difference between the differences:
Now we have a list of constants. If the first difference line is not constant but the second difference line is, the sequence is a quadratic sequence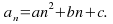
We start by find the first coefficient, of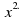 This is equal to the second difference line divided by 2:
This is equal to the second difference line divided by 2:
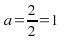
We now know the sequence is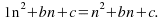 We Form an
We Form an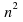 line (1 4 9 16 25) and find the difference between the original sequence and the terms of this line. This will give us another sequence: an arithmetic sequence.
line (1 4 9 16 25) and find the difference between the original sequence and the terms of this line. This will give us another sequence: an arithmetic sequence.
The difference is
The common difference is -1:
Because the common difference is -1 we know this sequence is a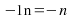 sequence. We construct a -1 times table and compare it with the arithmetic sequence (1):
sequence. We construct a -1 times table and compare it with the arithmetic sequence (1):
To get the sequence (1) from the -1 times table we have to add 2 so the arithmetic sequence is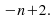 We add this to the
We add this to the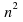 to get the n th term or rule for the quadratic sequence:
to get the n th term or rule for the quadratic sequence:
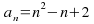
Example: Find the rule for the sequence: 5, 9, 17, 29, 45
Construct a first and second difference lines:
The second difference line is 4 so we know it is a 4 over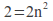 sequence. Form a
sequence. Form a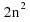 line and find the difference between this and the original quadratic sequence.
line and find the difference between this and the original quadratic sequence.
the difference is
This is an arithmetic or simple sequence. The common difference for this line is -2 so we have a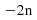 sequence. Form a -2 times table and find the difference between it and the arithmetic sequence.
sequence. Form a -2 times table and find the difference between it and the arithmetic sequence.
The difference is 5 so the arithmetic sequence is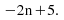 Add this to the
Add this to the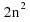 to get the formula for the n th term:
to get the formula for the n th term: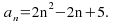
Add comment
![]()
![]() This is equal to the second difference line divided by 2:
This is equal to the second difference line divided by 2:![]()
![]() We Form an
We Form an![]() line (1 4 9 16 25) and find the difference between the original sequence and the terms of this line. This will give us another sequence: an arithmetic sequence.
line (1 4 9 16 25) and find the difference between the original sequence and the terms of this line. This will give us another sequence: an arithmetic sequence.![]() sequence. We construct a -1 times table and compare it with the arithmetic sequence (1):
sequence. We construct a -1 times table and compare it with the arithmetic sequence (1):![]() We add this to the
We add this to the![]() to get the n th term or rule for the quadratic sequence:
to get the n th term or rule for the quadratic sequence:![]()
![]() sequence. Form a
sequence. Form a![]() line and find the difference between this and the original quadratic sequence.
line and find the difference between this and the original quadratic sequence.![]() sequence. Form a -2 times table and find the difference between it and the arithmetic sequence.
sequence. Form a -2 times table and find the difference between it and the arithmetic sequence.![]() Add this to the
Add this to the![]() to get the formula for the n th term:
to get the formula for the n th term:![]()