Features of the Derivative Graph

• Print

Any function can be graph. When a function is differentiated, a derivative function is the result. This derivative function can be graphed, and features of the derivative graph may tell us something about the original graph. In particular, we can identify stationary points and determine their nature.

Suppose a functionhas derivativethe graph of which is sketched below.

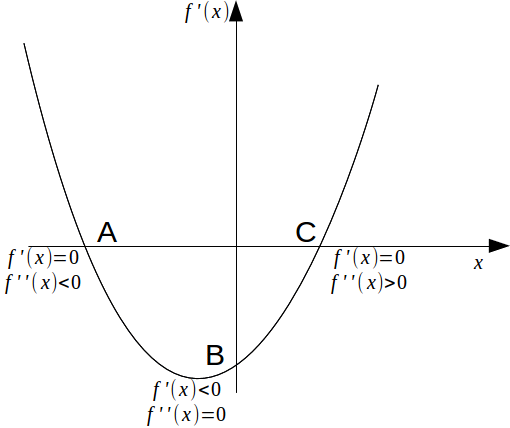
At the point A,so the point A is a stationary point forSincethe point A is a maximum.

At the point B,so the point B is a point of inflection forSincethe point B is a non stationary point of inflection.

At the point C,so the point C is a stationary point forSincethe point C is a minimum.

The graph below has three points of inflexion.

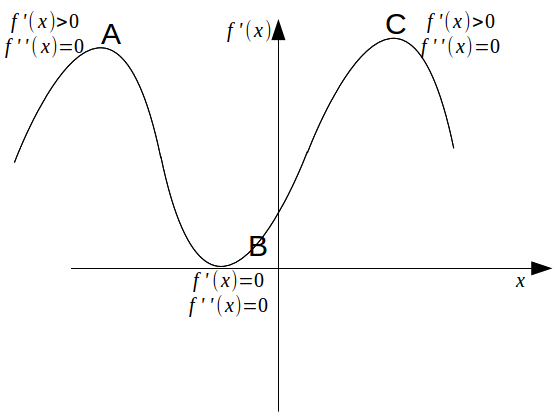
At the point A,so the point A is a point of inflexion forSincethe point A is a non stationary point of inflexion.

At the point B,so the point B is a point of inflection forSincethe point B is a stationary point of inflection.

At the point C,so the point C is a point of inflexion forSincethe point A is a non stationary point of inflexion.