\[x\]
.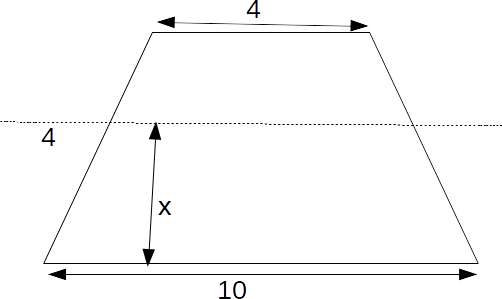
\[x\]
for the length \[l\]
of the cutting line. When \[x=0, \: l=10\]
and when \[x=4, \: l=4\]
.From these two,
\[l=10-1.5x\]
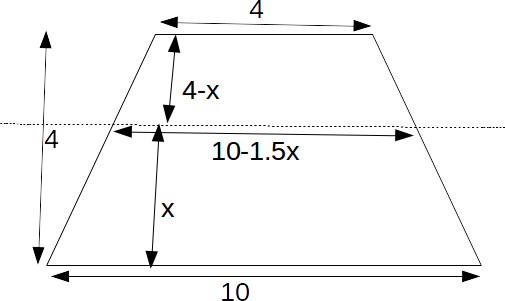
\[\frac{1}{2}(4+10-1.5x)(4-x)\]
The area of the part below the cutting line is
\[\frac{1}{2}(10+10-1.5x)x\]
Equating these gives
\[\frac{1}{2}(4+10-1.5x)(4-x)=\frac{1}{2}(10+10-1.5x)x\]
Expanding this and simplifying gives
\[3x^2-40x+56=0\]
Solving this equation gives
\[x= \frac{40 \pm \sqrt{928}}{6}\]
Obviously x must be less than the height of the trapezium so
\[x= \frac{40 - \sqrt{928}}{6}= x= \frac{20 - 2\sqrt{58}}{3}\]
since the other possibility gives \[x \gt 4\]
.