 We are to decide if the trapezium ABCD below is isosceles. One way of doing this is to check whether the line between the midpoints of the parallel sides is perpendicular to these sides - the gradients multiply to give
We are to decide if the trapezium ABCD below is isosceles. One way of doing this is to check whether the line between the midpoints of the parallel sides is perpendicular to these sides - the gradients multiply to give \[-1\]
. If it is, the trapezium is isosceles.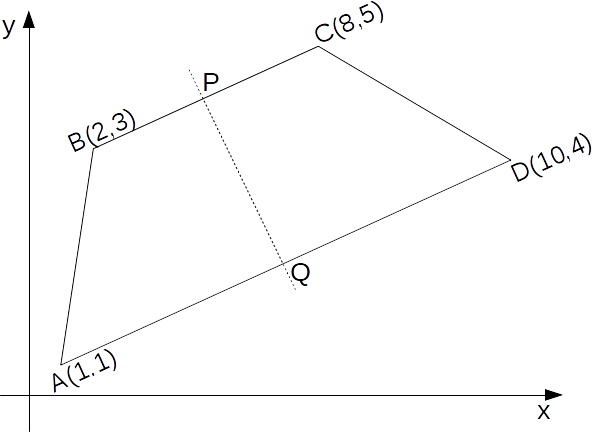
\[\frac{(2,3)+(8,5)}{2}=(5,4)\]
The midpoint of AD is point Q with coordinates
\[\frac{(1,1)+(10,4)}{2}=(5.5,2.5)\]
The gradient of QP is nbsp;
\[\frac{(4-2.5}{5-5.5}=\frac{1.5}{-0.5}=-3\]
The gradient of BC is nbsp;
\[\frac{(5-3}{8-2}=\frac{2}{6}=\frac{1}{3}\]
These gradients multiply to give
\[-1\]
so the trapezium is isosceles.