Furthest Distance of a Point on a Circle From the Origin
Suppose we have a circle and we want to find the greatest distance of any point on the circle from the origin. This point must lie on the straight line from the origin, through the centre of the circle, to the point, which is on the opposite side of the centre of the circle from the origin.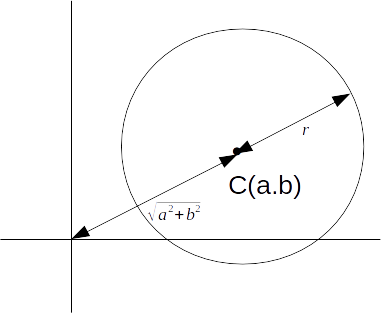
\[(x-2)^2+(y-3)^2=5^2\]
with centre \[(2,3)\]
and radius 5, the furthest distance is \[\sqrt{2^2+3^2}+5=\sqrt{13}+5\]
.