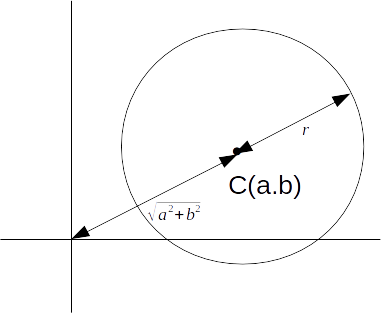
\[(x-2)^2+(y-3)^2=5^2\]
with centre \[(2,3)\]
and radius 5, the furthest distance is \[\sqrt{2^2+3^2}+5=\sqrt{13}+5\]
.The point is further from the origin than the centre of the circle, along the same line, by a factor
\[\frac{\sqrt{13}+5}{\sqrt{13}}\]
.Hence the coordinate of the point is
\[\frac{\sqrt{13}+5}{\sqrt{13}}(2,3)=\frac{13+5 \sqrt{13}}{13} (2,3)=(\frac{26+10 \sqrt{13}}{13}, \frac{39+15 \sqrt{13}}{13})\]
.