Proof of the Remainder Theorem

The remainder theorem states that when a polynomialis divided by a linear expressionthe remainder is

Example: Whenis devider bysubstituteto obtain the remainder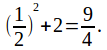

We can prove it quite easily by performing long division ofbyto obtain the quotientand remainderWe can write

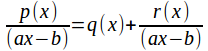
or equivalently

(1)

If the degree ofisthen the degree ofis and the degree ofmust be one less than the degree ofie the degree ofis 0 sois a constant. We can write

Now substitute

so thatas required.