\[x sin 60 = \frac{x \sqrt{3}}{2}\]
.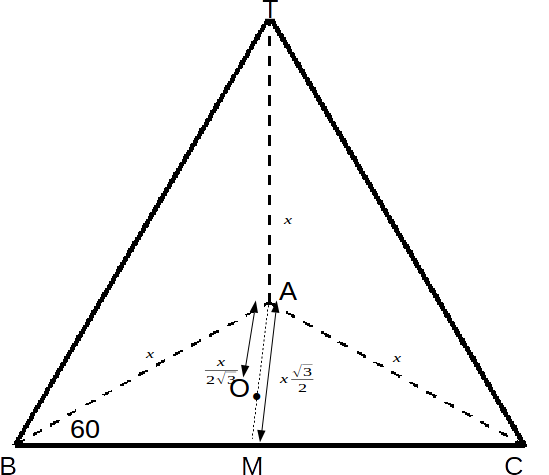
\[\frac{2}{3}\]
of the distance from A nto M ie \[\frac{2}{3} \times \frac{x \sqrt{2}}{3}= \frac{x}{\sqrt{3}}\]
.The centre of the sphere at the centre of the tetrahedron is vertically above the centre O of the triangle ABC and
\[\frac{1}{3}\]
of the height of the tetrahedron above the base, since a cross section of the tetrahedron seen from the side is a triangle, and the centre of a triangle is \[\frac{1}{3}\]
the distance from the centre of an edge to a vertex.The height OT of the triangle is
\[\sqrt{x^2 - (\frac{x}{\sqrt{3}})^2} = x \sqrt{\frac{2}{3}}\]
The radius of the tetrahedron is
\[\frac{1}{3} \times x \sqrt{\frac{2}{3}} = \frac{x}{3} \sqrt{\frac{2}{3}} \]