Side of a Square Inscribed in a Diamond
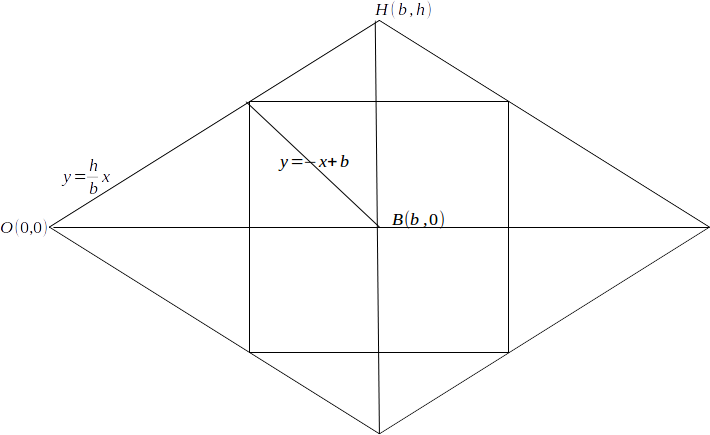
\[2h\]
and base \[2b\]
with vertex at the origin as shown will be foumd from the intersection of the lines \[y= \frac{h}{b} x, \: y= -x+b\]
\[\frac{h}{b} x=-x+b \rightarrow x( \frac{h}{b} + 1) = b \rightarrow x=\frac{b^2}{h+b} \]
The square will be of side
\[2(b - \frac{b^2}{h+b}) = \frac{2hb}{h+b}\]