Finding the Equation for the Angle Subtended By a Chord That Splits A Circle in a Ratio
Suppose we have a circle of radius\[r\]
with a chord. The chord cuts the circle into minor and major segments, with areas in the ratio 1:3. We can find an angle for the angle \[\theta\]
subtended by the chord AB.
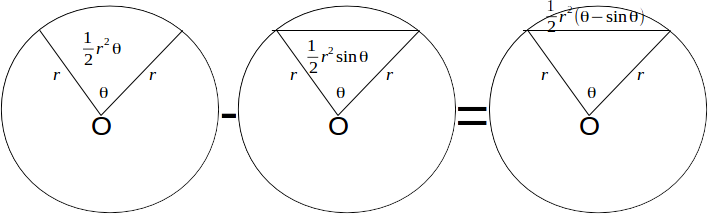
\[\frac{1}{2}r^2 \theta\]
and the area of the triangle is \[\frac{1}{2}r^2 sin \theta\]
&nbs[; where \[\theta\]
is in radians.The difference between these is the area of the minor segment:
\[A_{MINOR \: SEGMENT}=\frac{1}{2}r^2 \theta - \frac{1}{2}r^2 sin \theta = \frac{1}{2} r^2( \theta - \sin theta)\]
.Since the area of the circle is
\[\pi r^2\]
, the area of the major segment is \[\pi r^2 - \frac{1}{2} r^2( \theta - \sin theta)\]
.These are in the ratio 1:3 so
\[3 \times A_{MINOR \: SEGMENT}= A_{MAJOR \: SEGMENT}\]
Hence
\[3 \frac{1}{2} r^2( \theta - \sin theta)=\pi r^2 - \frac{1}{2} r^2( \theta - \sin theta)\]
Dividing by
\[r^2\]
gives \[3 \frac{1}{2}( \theta - \sin theta)=\pi - \frac{1}{2} ( \theta - \sin theta)\]
Adding
\[\frac{1}{2} ( \theta - \sin theta)\]
to both sides:\[4\frac{1}{2} ( \theta - \sin theta)= \pi\]
Hence
\[2 ( \theta - \sin theta)= \pi\]