A function of
is any formula withalone in it as a variable, so that a value may be chosen for
and the value of the function calculated for this value of
Functions have the following properties:
For a given value ofthere is only one value of a function
A function may have one value for different values of
A function may be defined for only certain values ofcalled the domain.
The set of all values that a function may take is called the range or codomain of the function.
For every function we may plot elements of the domain against elements of the codomain ie points
A function is defined entirely by it's form. For example, if
then 
This expression may be simplified, but still represents the same function.
Examples of functions ofinclude:
Notice that a function may be labelled by
Ifis not present in the notation then it is understood that the variable is
If the graph of
againstis shown then the domain and range of the function may be read off the graph.
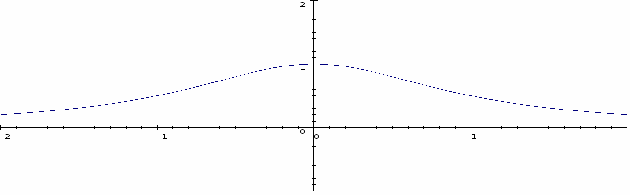
The diagram shows the graph of
The domain is
and the range is
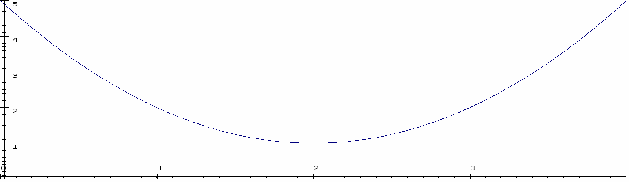
The diagram shows the graph of
The domain is
and the range is