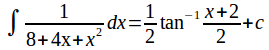Integration Using Two Substitutions

If an integral can be evaluated using the substitution method, it of often simpler to make two substitutions. The first seeks to simplify the integrand into a more familiar form which.

Example:

Complete the square inside the square root to obtain

Now substituteThe integral becomes

Now substituteThe integral becomes

This can be evaluated using the trigonometric identityrearranged asWe have

Now use the substitutions to obtain the result in terms of x. Useand

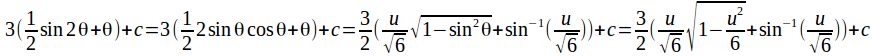Now use u=x+1 to obtain the result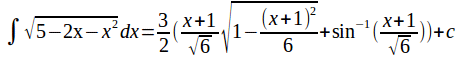

Example: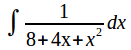

Complete the square inside the square root to obtain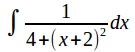

Now substituteThe integral becomes

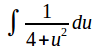
Now substituteThe integral becomes

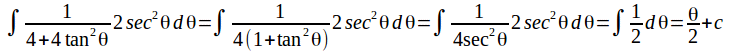
Useandsuccessively to obtain