We start with a graph![]() If the graph is rotated about the
If the graph is rotated about the![]() axis it traces out a surfaces as shown. Between the surface and the
axis it traces out a surfaces as shown. Between the surface and the![]() – axis we may form a solid. We show here how to find the volume of this solid.
– axis we may form a solid. We show here how to find the volume of this solid.
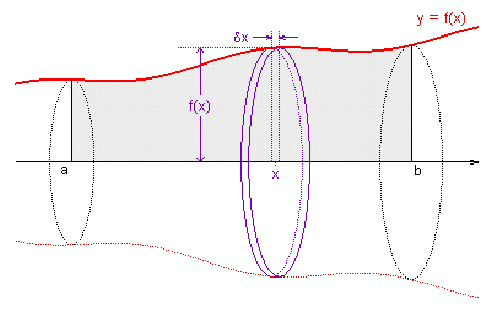
We may picture the solid as being made up of slices of solid. For the function![]() each slice is a disk of radius
each slice is a disk of radius![]() and thickness
and thickness![]() and has volume
and has volume![]() By summing these slices, obtaining
By summing these slices, obtaining![]() we get an approximate value for the volume. The value becomes exact
we get an approximate value for the volume. The value becomes exact![]() turning the summation into an integral. Hence, if a curve between the values of
turning the summation into an integral. Hence, if a curve between the values of![]() and
and![]() is rotated about the
is rotated about the![]() - axis, the volume of the solid formed is
- axis, the volume of the solid formed is![]() (1)
(1)
If we have a curve![]() which we rotate about the
which we rotate about the![]() - axis between
- axis between![]() and
and![]() the volume of the solid formed is
the volume of the solid formed is![]() (2) obtained from (1) by interchanging
(2) obtained from (1) by interchanging![]() and
and![]()
Example: The curve![]() is rotated about the
is rotated about the![]() – axis. Find the volume of the solid formed.
– axis. Find the volume of the solid formed.
![]()
We can integrate by using the identity![]() to give
to give
![]()
Example: The graph![]() is rotated about the
is rotated about the![]() - axis. Find the volume of the solid formed.
- axis. Find the volume of the solid formed.
![]() We evaluate:
We evaluate:
![]()