It is very easy to solve linear inequalities of the form![]() almost as easy as solving linear equations:
almost as easy as solving linear equations:![]() Solving an absolute inequality, where the equation includes modulus signs is a little bit trickier. When we remove the minus sign it can be hard to work out which way the inequality signs point. Given this, the safest way to solve these equations is either to sketch both absolute functions so that you can see graphically which way the modulus signs point, or square both sides, making both sides positive even without the need for the modulus brackets, then factorising and solving the resulting quadratic inequality.
Solving an absolute inequality, where the equation includes modulus signs is a little bit trickier. When we remove the minus sign it can be hard to work out which way the inequality signs point. Given this, the safest way to solve these equations is either to sketch both absolute functions so that you can see graphically which way the modulus signs point, or square both sides, making both sides positive even without the need for the modulus brackets, then factorising and solving the resulting quadratic inequality.
Example: Solve![]()
Squaring both sides gives![]() We expand the brackets and simplify to give
We expand the brackets and simplify to give![]() Now move every term to the right hand side to give
Now move every term to the right hand side to give![]() We can divide by the common factor non zero 3 to obtain
We can divide by the common factor non zero 3 to obtain![]() The quadratic factorises to give
The quadratic factorises to give![]() The graph
The graph![]() is illustrated below.
is illustrated below.
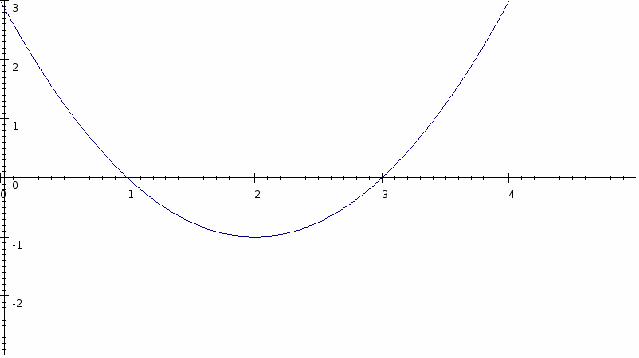
We want those values of![]() for which
for which![]() ie
ie![]() hence the set of values of
hence the set of values of![]() satisfying
satisfying![]() is given by
is given by![]()
If instead the question had asked to solve![]() we would have had solved
we would have had solved![]() so that
so that![]() or
or![]() Notice that now the set of
Notice that now the set of![]() consists of two intervals.
consists of two intervals.