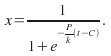The Logistic Equation
The equation takes a certain form and is used in many models, including the spread of diseases, discussed here. It is based on two assumptions
Since each infected person is capable of passing on the disease, the rate of spread of the disease is proportional to the infected population
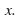
Since the disease may only be transmitted to uninfected people, the rate of spread of the disease is proportional to the number of uninfected people
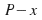 where P is the total population.
where P is the total population.
Hence the rate of spread of the disease is proportional to the product of these two:![]()
We separate the variables to obtain![]() and then separate into partial fractions.
and then separate into partial fractions.
![]()
Multiply by x(P-x), clearing all the fractions, to obtain![]()
![]()
![]() hence
hence ![]() We integrate:
We integrate:
![]()
The general solution of the logistic equation is given by t={k over P}ln({x over {P-x}) +C. This equation will give the time for any know population x. We can rearrange it to make x the subject:
![]()
We remove the ln by exponentiating both sides:![]()
Now clear the fraction by multiplying by P-x to obtain
![]()
Now divide by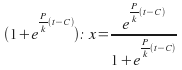
The final, possibly unnecessary step is to multiply numerator and denominator by![]() to give
to give