We start with a graph
If the graph is rotated about the
axis it traces out a surfaces as shown. Between the surface and the– axis we may form a solid. We show here how to find the volume of this solid.
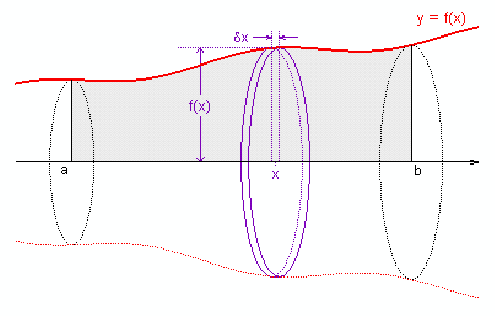
We may picture the solid as being made up of slices of solid. For the function
each slice is a disk of radius
and thickness
and has volume
By summing these slices, obtaining
we get an approximate value for the volume. The value becomes exact
turning the summation into an integral. Hence, if a curve between the values of
and
is rotated about the- axis, the volume of the solid formed is
(1)
If we have a curve
which we rotate about the- axis between
and
the volume of the solid formed is
(2) obtained from (1) by interchangingand
Example: The curve
is rotated about the– axis. Find the volume of the solid formed.
We can integrate by using the identity
to give
Example: The graph
is rotated about the- axis. Find the volume of the solid formed.
We evaluate:
