Complete Graphs
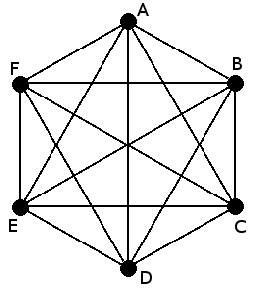
A complete graph is such that every pair of vertices must be connected by a single edge.
The above diagram is of a complete graph with 6 vertices.
We can to find out the total number of edges in this graph.
We could list all possible edges in terms of the vertices they connect.:
AB, AC, AD, AE, AF
BC, BD, BE, BF
CD, CE, CF
DE, DF
EF
Note that we include AB but not BA as this would be counting the same edge twice.
There are 5+4+3+2+1=15 edges in the above graph.
Of course, with a set that has many more than 6 elements, you probably wouldn’t want to list all possible pairs. Thankfully there is another, easier way to work out the number of edges in a complete graph, using binomial coefficients. We want the number of ways we can pick two elements from a set of n.
![]()
By using either the formula above, or by counting pairs, we see that the total number of possible pairs in the set is 15. This is the same as the total number of edges in the complete graph for that set.