Dijkstra’s algorithm is used to find the shortest path tree from a given node to any (or every) other node in a network.
Dijkstra’s algorithm requires that each node in the network be assigned values (labels). The labels are assigned in order of distance from the starting point, with the labels assigned as we work our way through the network. There is a working label and a permanent label, as well as an ordering label. The smallest working label ateach iteration will become permanent.
The steps of Dijkstra’s algorithm are:
-
Give the start point the permanent label of 0.
-
Any vertex directly connected to the last vertex given a permanent label is assigned a working value equal to the weight of the connecting edge added to the permanent value of the node you are coming from. If it already has a working value replace it only if the new working value is lower.
-
Select the minimum current working value in the network and make it the permanent value for that node.
-
If the destination node has a permanent label go to step 5, otherwise go to step 2.
-
Connect the destination to the start, working backwards. Select any edge for which the difference between the permanent labels at each end is equal to the weight of the edge.
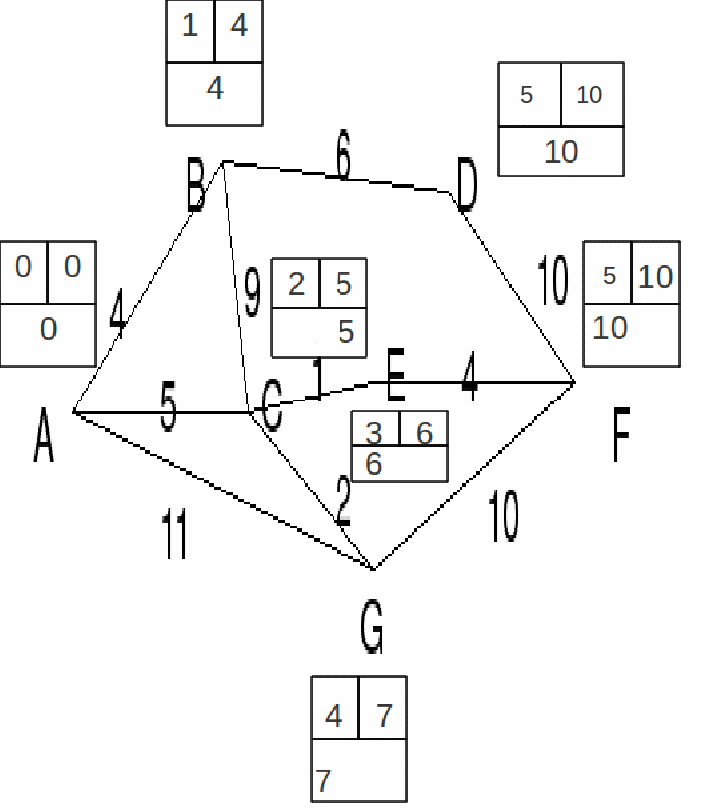
In this example we will consider the network in the diagram below. We would like to find the shortest path from node A to node F.
It is a good idea to use a system for keeping track of the current working labels and the ordering and permanent labels of each of thenodes in the network. A small grid is drawn near each of the nodes, working labels are written in the lower box, ordering labels in the upper right box.
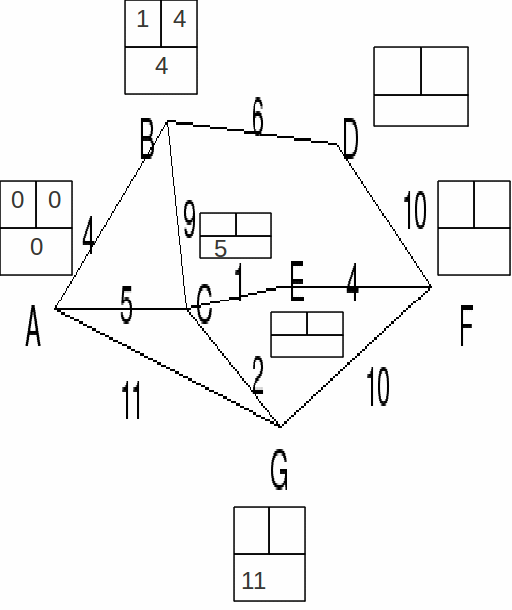
Node A is labelled 0. The distance from A to A is 0. The closest to A is B, distance 4 from A, so B is labelled 1.
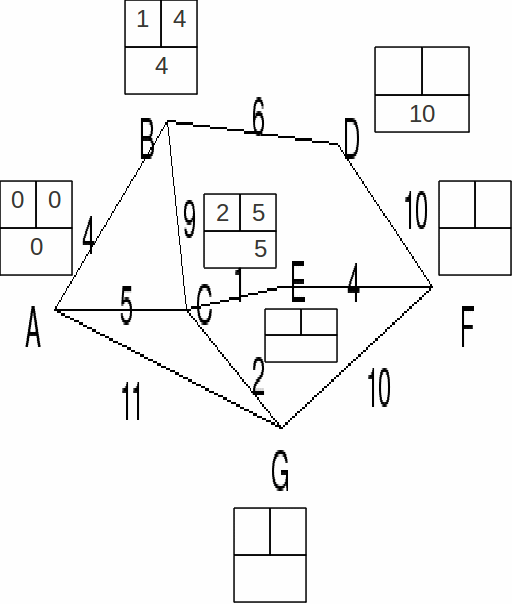
C and D are directly connected to B. The working value is of D is 4+6=10 and the working calue of C is 4+9=13. A lesser distance 5 from A exists for C, and this becomes the permanent value. Node C has label 2.
E and G are directly connected to C. The closest to C is E, distance 6 from A. E is labelled 3.
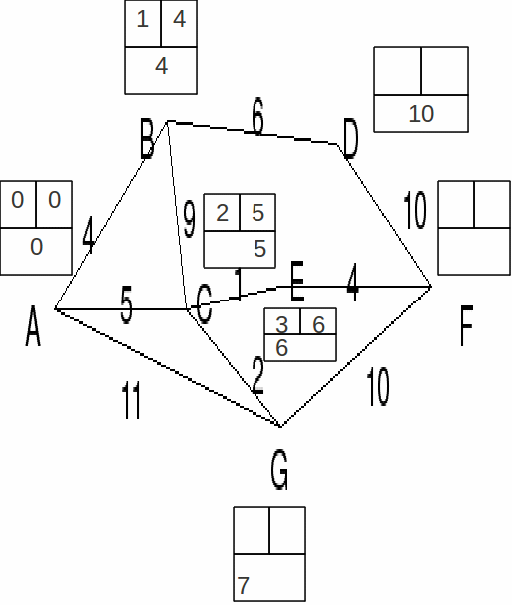
E is connected to F.
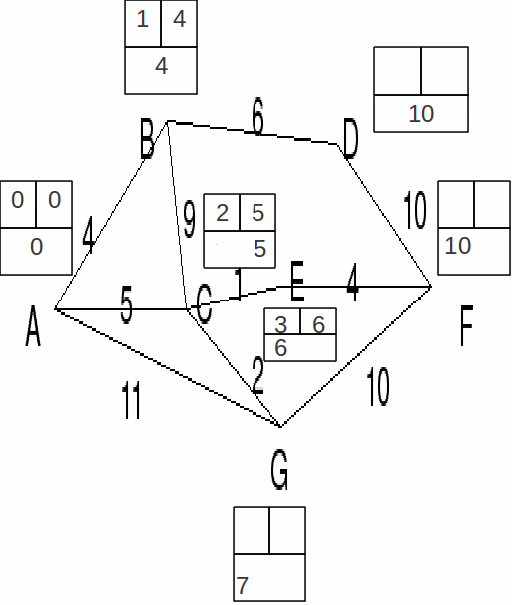
By inspection all the distances are minimised and we can label the remaining nodes.