Graphical Representation of Method to Find Optimal Strategy for Two Player Game

Suppose we have the payoff matrix below for player B in a two player game between players A and B.

If player B chooses strategy U with probabilityand strategy V with probability and if A chooses strategy Y, the expected gain for B is

If A chooses strategy Z, the expected gain for B is

We can plot these two functions. The point of intersection will give the proportion of the time that player B choose strategy U.

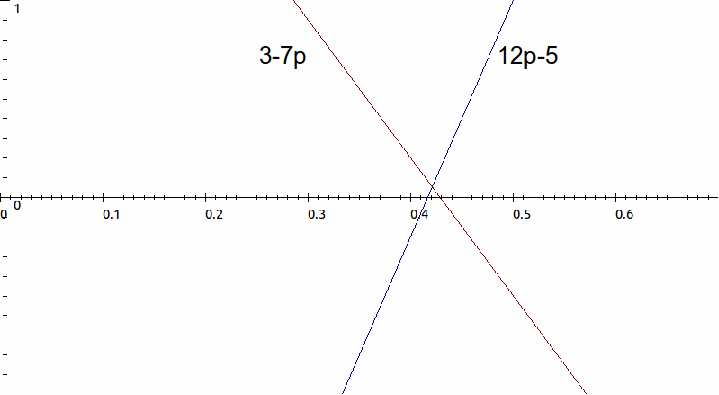
The optimal value foroccurs when these expected gains are equal, so

We can find the probability that player A should choose strategies Y and Z similarly.

Suppose that player A chooses strategy Y with probabilityand strategy Z with probability

Then if B chooses strategy U, the expected loss for A is

If B chooses strategy V, the expected loss for A is

We can plot these. The intersection give give the the proportion of games in which player A should play strategy Y.

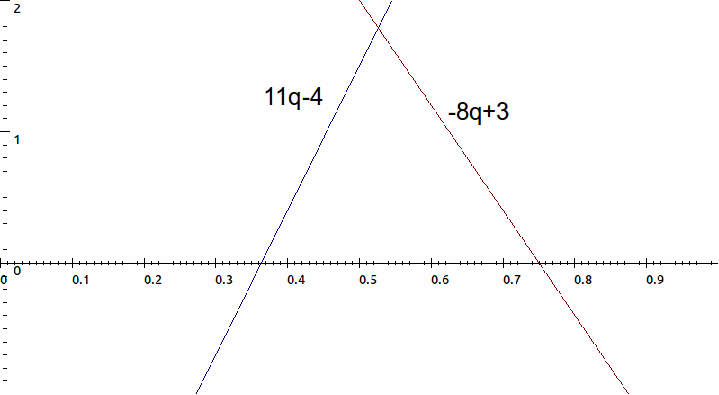
The optimal value forwhich minimises the losses for play A, occurs when these expected losses are equal, so