For a two player, zero sum game, a stable solution is one such that each player always plays the same, unchanging strategy. The Stable Solution Theorem states that there will only be a stable solution when the row maximum of the matrix representing the playoffs for one player equals the column minimum.
If the matrix represents the payoffs for![]() of each combinations of strategies of each player, with
of each combinations of strategies of each player, with![]() and
and![]() player A's and B's play safe winnings respectively, then
player A's and B's play safe winnings respectively, then
-
For any zero sum game,
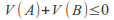
-
A zero sum game has a stable solution if and only if
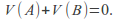
Prove 1 first. If both players play safe then![]() wins at least
wins at least![]() and
and![]() wins at least
wins at least![]() so the total winnings are at least
so the total winnings are at least![]() but in a zero sum game the total winnings are always zero so
but in a zero sum game the total winnings are always zero so![]()
Since![]() is the row maximin there is a row in which the smallest element is
is the row maximin there is a row in which the smallest element is![]() If the row is the kth row then player
If the row is the kth row then player![]() will be playing safe by playing strategy
will be playing safe by playing strategy![]() Similarly
Similarly![]() is the column minimax, there is a column minimax, there is a column, say the lth, in which the largest entry is
is the column minimax, there is a column minimax, there is a column, say the lth, in which the largest entry is![]() Player
Player![]() will be playing safe by choosing strategy
will be playing safe by choosing strategy![]()
The value of the game to![]() is given by the element
is given by the element![]() in the matrix.
in the matrix.![]() since
since![]() is the smallest number in row
is the smallest number in row![]() and
and![]() since
since![]() is the biggest number in column
is the biggest number in column![]() Hence
Hence
![]()
but![]() hence
hence![]() hence
hence![]() and
and![]()
![]() is then the smallest in row
is then the smallest in row![]() and the biggest in column
and the biggest in column![]()
Player![]() assumes that player
assumes that player![]() will play strategy
will play strategy![]() There is no benefit to
There is no benefit to![]() in changing strategy since
in changing strategy since![]() gives the biggest payoff to
gives the biggest payoff to![]()
![]() also assumes that
also assumes that![]() will play strategy
will play strategy![]() There is no benefit to
There is no benefit to![]() in changing strategy since
in changing strategy since![]() gives the biggest payoff to
gives the biggest payoff to![]() so
so![]() will always play strategy l. The game is table and
will always play strategy l. The game is table and![]() is the saddle point.
is the saddle point.
To prove the 'only if' part, note that if the game is stable there is a saddle point or possibly points that give the game's value. Since this is a zero sum game this must be equal and opposite for each player so![]()