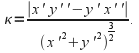The Derivation of the Curvature Formulae

If we have an arc of a circle, the length of the arc isthe radius of the circle isand the angle subtended by the arc isthenand the radiusThe curvature of the circle isWe can generalise this idea to find the curvature of a curve at any point on the curve by taking the limit asand

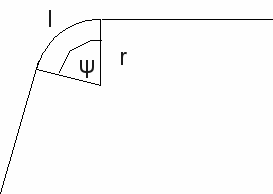
If a curve is the graph of a twice differentiable functionthen the curvature can be calculated from the formula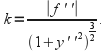

Proof:so

Differentiate with respect tousing the chain rule:(1)

Ifis the length of a small piece of curve then

Substitute this into (1) to obtain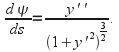after some rearrangement. Take the magnitude of both sides to obtain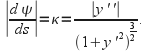

For a curve given in parametric coordinates the curvature is given by