The sum of a series may not be easily found, and it is desirable to be able to find upper and lower limits for its value. If series consists of terms that are decreasing or decreasing then it may be possible to easily find a bound by integration.
To find the bounds for![]() note that
note that![]() is an increasing function. To find a lower bound divide the interval of integration
is an increasing function. To find a lower bound divide the interval of integration![]() into
into![]() intervals
intervals![]()
![]() The minimum value of
The minimum value of![]() on each interval
on each interval![]() is
is![]() The area of the (k-1)th rectangle is {1 over n}e^{-{n over k}} .
The area of the (k-1)th rectangle is {1 over n}e^{-{n over k}} .
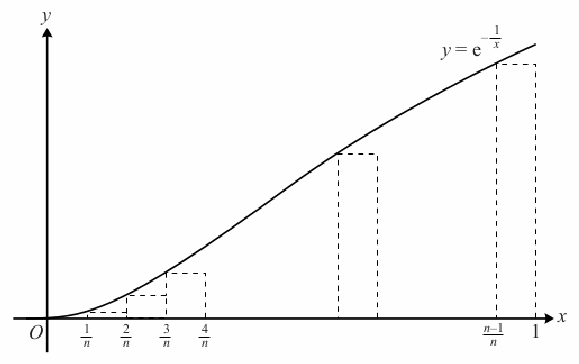
Hence![]()
To find an upper bound for the integral note that the maximum value of![]() on each interval
on each interval![]() is
is![]() The area of the
The area of the![]() th rectangle,
th rectangle,![]() is
is![]()
Hence![]()
Hence we can write![]()