Odd and Even Functions

A functionis odd isand even if

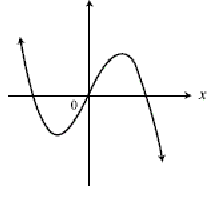
The function above is odd. Every odd function has rotational symmetry order two about the origin, so we can rotate it by

is odd since

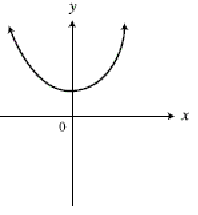
The function above is even. Every even function is symmetric with respect to the y – axis, so it will be the same graph after reflection in the y - axis.

is even since

Every arbitrary function can be expressed as a sum of odd and even functions.

is an odd function since

is an even function since

Products of odd and even functions obey similar laws to the sign laws for multiplying positive and negative numbers.

even*even=even

odd*odd=even

odd*even=odd

even*odd=odd

There are also laws for composing odd and even functions

even(even)=even since

odd(odd)=odd since

even(odd)=even since

odd(even)=even since