Odd and Even Functions
A function
is odd is
and even if
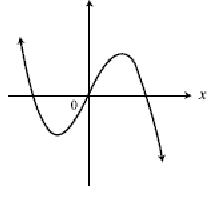
The function above is odd. Every odd function has rotational symmetry order two about the origin, so we can rotate it by
is odd since
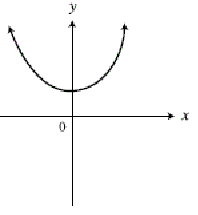
The function above is even. Every even function is symmetric with respect to the y – axis, so it will be the same graph after reflection in the y - axis.
is even since
Every arbitrary function can be expressed as a sum of odd and even functions.
is an odd function since
is an even function since
Products of odd and even functions obey similar laws to the sign laws for multiplying positive and negative numbers.
even*even=even
odd*odd=even
odd*even=odd
even*odd=odd
There are also laws for composing odd and even functions
even(even)=even since
odd(odd)=odd since
even(odd)=even since
odd(even)=even since