Complex Fractions
Typically we have to express a complex fraction![]() in the form
in the form![]() We do this by multiplying top and bottom by the complex conjugate of the denominator, remembering that
We do this by multiplying top and bottom by the complex conjugate of the denominator, remembering that![]() The complex conjugate of
The complex conjugate of![]()
Example: Express![]() in the form
in the form![]()
![]()
![]()
Argand Diagrams
We may also have to plot complex numbers on an Argand diagram. This is a normal set of![]() axes:
axes:![]() is plotted as the point
is plotted as the point![]() In the diagram below the complex number
In the diagram below the complex number![]() s plotted as the point
s plotted as the point![]()
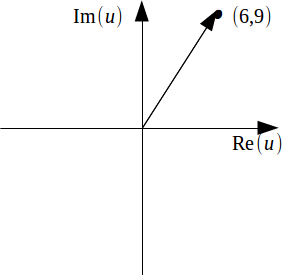
Magnitudes, Arguments and the Polar Form of Complex Numbers
The magnitude of![]()
the argument of![]()
The polar form of![]() is written as
is written as![]()
Multiplying Complex Numbers
Given two complex numbers![]() and
and![]() we can find the product
we can find the product![]()
We can express this in polar form as above,![]()
![]()
then![]()
Or we can express![]() and
and![]() in polar form then using the normal rules for multiplying exponentials:
in polar form then using the normal rules for multiplying exponentials:
![]()
![]()
![]()
so![]()
![]()
Dividing Complex numbers
We can use the method of the top of the page to express in cartesian form, or, if we require polar form, using the normal rule for dividing exponentials:
![]()