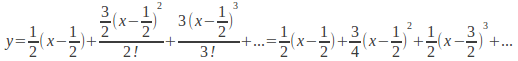If the exact solution to a differential equation cannot be found one method of solving the equation is by repeated differentiation to find a Taylor series for the solution. In general the series will involve the introduction of constants, but these can be found if we have some initial or boundary conditions for the solution.
For example, if![]() with
with![]() then we can find the first two terms in the Taylor series
then we can find the first two terms in the Taylor series
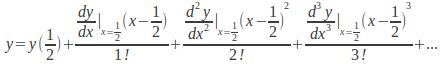
using the differential equation itself. We are given![]() and can rearrange the equation to give
and can rearrange the equation to give![]() Substitute
Substitute![]() and
and![]() to get
to get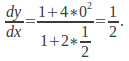
then![]()
We can get the third and fourth terms by differentiating the differential equation to give
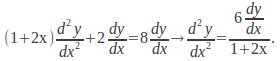
Substitute![]() and
and![]() to get
to get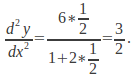
Now differentiate![]() to get
to get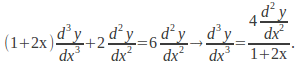
Substitute![]() and
and![]() to get
to get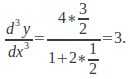
Then