Typically a curve is given in polar coordinates![]() with
with![]() as a function of
as a function of![]() It is often quite simple to write this in cartesian coordinates
It is often quite simple to write this in cartesian coordinates![]() by making the substitutions
by making the substitutions![]() and simplifying the resulting expression.
and simplifying the resulting expression.
Example:![]()
![]() On substituting these, the equation becomes
On substituting these, the equation becomes![]()
Subtract the terms on the right hand side to give![]()
We can complete the square for both the![]() 's and
's and![]() 's to give
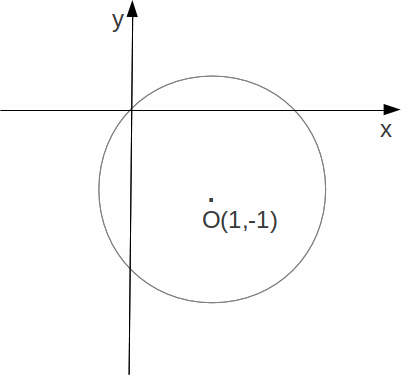
's to give![]() This is the equation of a circle with centre
This is the equation of a circle with centre![]() and radius 2. Note that
and radius 2. Note that![]() satisfies the cartesian equation so lies on the curve.
satisfies the cartesian equation so lies on the curve.