Finding Factors in the Determinant of a Matrix
Often the determinant of a matrix may be written as a product of one or more factors. We can find an expression for the determinant andfactorise it, which may be long and tedious, or we may look at the matrix itself and see which changes we can make so that the matrix becomes linearly independent (if it isn't already).
Example: Find factors in the determinant of the matrix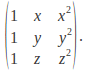
The determinant is![]() (1)
(1)
If![]() then the matrix becomes
then the matrix becomes
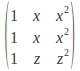
The first two rows are the same and the determinant is zero, so![]() is a factor.
is a factor.
If![]() then the matrix becomes
then the matrix becomes
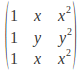
The first and third rows are the same and the determinant is zero, so![]() is a factor.
is a factor.
If![]() then the matrix becomes
then the matrix becomes
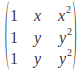
The last two rows are the same and the determinant is zero, so![]() is a factor.
is a factor.
The matrix can have at most three factors (since it has three rows) so![]() is a factor and can differ from the determinant only by a constant factor. In fact, multiplying out the above expression gives
is a factor and can differ from the determinant only by a constant factor. In fact, multiplying out the above expression gives![]() This differs from (1) only by a factor -1 so the determinant can be factorised as
This differs from (1) only by a factor -1 so the determinant can be factorised as![]()