Using Vectors to Find the Centres of Shapes

We can label the sides of polygons with letters that represent vectors. The length of the vector is (typically) the length of the side and the direction of the vector is along the side. We can often use vectors to determine the centre of the shape. Suppose for example that we want to find the centre of a triangle ABC. We label the side AC asand the side AB asConstruct then the parallelograms ABCD and AEBC as below.

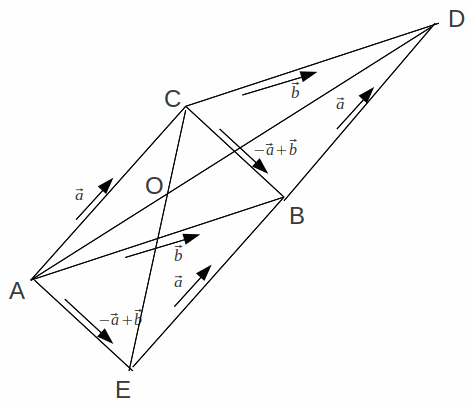
The centre of the triangle lies on the diagonal AD of the parallelogram ABCD and the diagonal CE of of the parallelogram AEBC.

We can find the equations of these diagonals using the general form for the vector equation of a line:

Take A as the origin, then the equation of AD is

C has the position vectorand CE has the direction vectorso the equation of CE is

Equatingandgives

Equating coefficients ofgives

Equating coefficients ofgives

Solving these simultaneous equations givesThis shows that the centre of a triangle is one third of the way from a vertex to the centre of the opposite side.