Simple harmonic motion occurs when motion in a circle with uniform acceleration is projected on a line through the centre of the circle. The motion is most naturally projected onto the x and y axes.
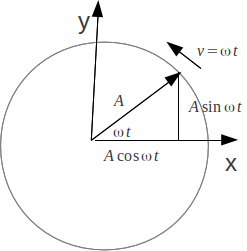
Suppose the motion is projected onto the![]() – axis. Then
– axis. Then![]() (1)
(1)
We can differentiate to obtain the velocity:![]() (2)
(2)
and again to get the acceleration:![]() (3)
(3)
We can write (3) as![]() so
so![]()
This is often taken as the basic equation of simple harmonic motion, and means that the the acceleration is proportional to the acceleration, but directed towards the zero point on the![]() – axis.
– axis.
We can use the identity![]() to obtain further equations.
to obtain further equations.
From (1)![]() and from (2)
and from (2)![]()
Substituting these into the identity gives![]()
Similarly for projection onto the![]() – axis:
– axis:![]() (4)
(4)
We can differentiate to obtain the velocity:![]() (5)
(5)
and again to get the acceleration:![]() (5)
(5)
We can write (5) as![]() so
so![]()
We can use the identity![]() to obtain a further equation.
to obtain a further equation.
From (4)![]() and from (5)
and from (5)![]()
Substituting these into the identity gives![]()
If the frequency is![]() then
then![]() so we can also write
so we can also write
![]() and
and![]() with corresponding equations for
with corresponding equations for![]()