The Centre of Mass of a Scalene Triangle
Equilateral and isosceles triangles of constant mass per unit area have symmetry, and this symmetry can be used to find the centre of mass of a triangle. The centre of mass of an equilateral triangle is quickly found to be two thirds of the distance from the vertex to the centre of the the opposite side, by a simple rotation argument,
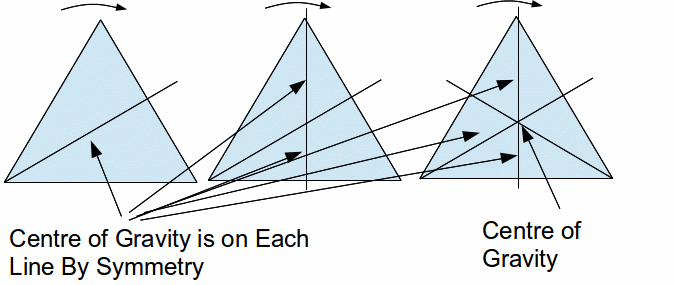
and the same result can be proved for an isosceles triangle by integration, taking moments about the odd side.
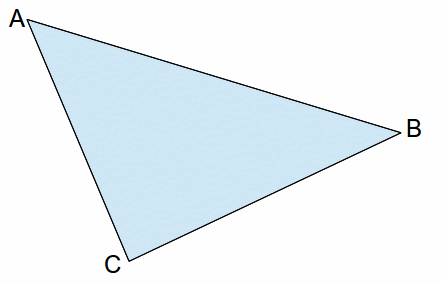
For a scalene triangle no symmetry argument is possible, and integration is tedious, but a vector argument can be made. Consider the triangle ABC below.
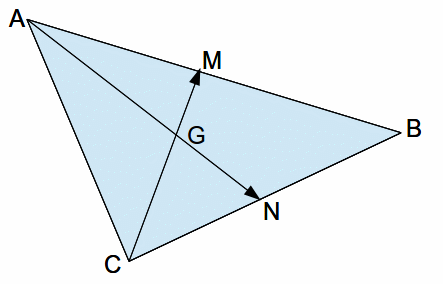
When a line is drawn through a vertex to the opposite side through the centre of gravity, half the area of the triangle must lie on either side, so the line drawn must bisect that side. Draw lines from A and C to the centres of the opposite sides, N and M respectively. These lines must intersect at the centre of gravity of the triangle, G below.
 >
>
![]() And since G is on
And since G is on![]()
![]() but
but![]() so
so![]()
and![]()
Taking C as the origin, the position vector of G is![]() or
or![]()
Equating these gives![]()
Now equate coefficients of![]()
Equate coefficients of![]()
equating these simultaneously gives![]() and the centre of gravity is two thirds of the way from any vertex to the centre of the opposite side.
and the centre of gravity is two thirds of the way from any vertex to the centre of the opposite side.