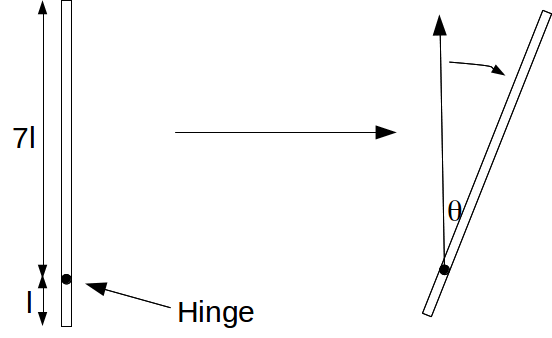
If a rod AB of length
and mass
is smoothly hinged at a point a distance
from the end A and, held with the end B above A and then given a small push so that it is free to rotate, we can apply conservation of energy to obtain the angular velocity
of the rod after it has turned through an angle
The moment of inertia of a rod of length
and mass M about its centre is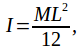
so the moment of inertia of the rod above about its centre is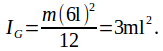
The parallel axis theorem states that if it is pivoted about a parallel axis a distance
(equal to
in this case) from the first, the moment of inertia about that point is
The kinetic energy of the rad at an time is
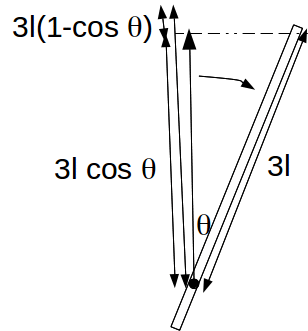
When the rod has turned through an angle
the centre of mass has fallen a distance
(see the diagram which shows the changing position of the centre of mass).
The increase in kinetic energy is equal to the loss in gravitational potential energy.
(1)
Taking moments about the hinge give
where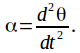
This is the same equation as obtained by differentiating (1) with respect to t.
Divide by
and put
The result is