Second order differential equations arise naturally as a result of applying Newton's second law of motion. If no external forces act then the equation may take the form
![]()
where![]() is a drag or resistance term and
is a drag or resistance term and![]() is a restoring force.
is a restoring force.
If there is no resistance term then the equation becomes![]() - the equation of simple harmonic motion - and this equation has the solution
- the equation of simple harmonic motion - and this equation has the solution![]()
If there is no restoring force the the equation becomes![]()
We can write this equations as![]()
Integration gives![]() We can solve this equation by separation of variables
We can solve this equation by separation of variables
![]()
Integration gives![]() and solving for x gives
and solving for x gives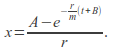
If there are both resistance and restoring terms then there are three possibilities.
We can substitute![]() so that
so that![]() and
and![]() The equation becomes
The equation becomes
![]()
We can divide by![]() (since an exponential is never zero) to obtain
(since an exponential is never zero) to obtain
![]()
This is a quadratic equation with roots![]()
If![]() then there are two distinct real roots
then there are two distinct real roots![]() and
and![]() and
and![]()
If![]() then there is one root
then there is one root![]() and
and![]()
In both of these cases,![]() may increase without limit if
may increase without limit if![]() is positive, and the motion is non – oscillatory.
is positive, and the motion is non – oscillatory.
If![]() then there are two distinct complex roots
then there are two distinct complex roots![]()
and![]() and
and![]()
This last solution for![]() represents oscillatory motion. If
represents oscillatory motion. If![]() the oscillations decay and if
the oscillations decay and if![]() the oscillations increase in size.
the oscillations increase in size.