If a manufacturer claims superiority for any of their products or a great deal rests the proportion of components that exceed a certain lifetime, then that claim or proportion probably needs to be tested for legitimacy or accuracy.
We can test a wide range of statistical parameters or models by subjecting it to a hypothesis test. We assume that the claim is true. The trueness of the claim forms the basis of the null hypothesis, and our suspicion that the claim is false forms the basis of the alternative hypothesis. We test an observation assuming that the null hypothesis is true, and calculate the probability of observing an outcome at least as unlikely as the observed outcome. If the probability of observing any outcome at least as unlikely is above a certain level, then we say there is insufficient level to reject the null hypothesis, and if the probability of observing any outcome at least as unlike is below that level, we reject the null hypothesis since the probability of observing that outcome is so unlike assuming the null hypothesis to be true. If a claim of superiority or safety issue is involved, then typically we are only interested in disproving the claim, or finding if safety is compromised, and we conduct a one tailed test.
Suppose for example that a manufacturer claims that their brand of cat food is preferred by 80% of cats. A suspicious cat lovers group finds that of the cats belonging to their members, only half prefer the manufacturers pet food over a rival brand. If the manufacturers claim is true, then any sample of twenty cats will produce the probabilities for the number of cats who prefer the manufacturers claim shown below.
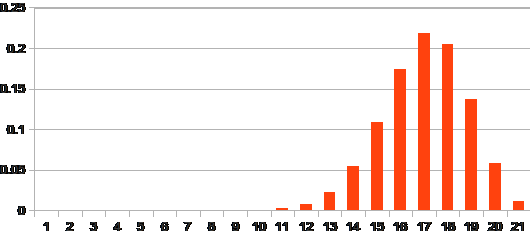
Suppose we decide to reject the claim if the probability of the manufacturers claim being true – or any more extreme outcome – is less than 5% or 0.05, given that we have observed only ten cats preferring the manufacturers petfood.
P(x <=10)=0.00259 <0.05, so the manufacturers claim is rejected, and there is some evidence that their brand of catfood is not preferred by 80% of all cats.