A probability distribution is usually defined in terms of it's probability distribution function (if continuous), the probability that it takes a value in a certain range, or probability mass function (if discrete), the probability that it takes a certain value. Sometimes it is more convenient to define it in terms of a cumulative distribution function.
If the probability density function for![]() where
where![]() may be finite or
may be finite or![]() and
and![]() may be finite or
may be finite or![]() is given by
is given by![]() then the cumulative distribution function, cdf, such that
then the cumulative distribution function, cdf, such that![]() is given by
is given by
![]() if
if![]() is continuous
is continuous
![]() if X is discrete.
if X is discrete.
Example: The continuous quantity![]() is uniformly distributed over the interval
is uniformly distributed over the interval![]() The probability distribution is
The probability distribution is![]() The cumulative distribution function is
The cumulative distribution function is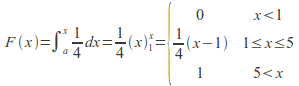
Example: The probability distribution of a random variable![]() is given in the following table. Construct the cumulative distribution function.
is given in the following table. Construct the cumulative distribution function.
|
|
0 |
1 |
2 |
3 |
4 |
5 |
|
|
0.10 |
0.05 |
0.00 |
0.25 |
0.15 |
0.45 |
To find the cumulative distribution function, add up the entries in the![]() row as you go along, to give
row as you go along, to give
|
|
0 |
1 |
2 |
3 |
4 |
5 |
|
|
0.10 |
0.15 |
0.15 |
0.40 |
0.55 |
1.00 |
Conversely given a cumulative distribution function we can find the probability distribution function by differentiation, or by subtraction each![]() from the previous one to give
from the previous one to give![]() in the case of a discrete distribution.
in the case of a discrete distribution.
Example: If![]() then
then![]()
Example:![]() is given in the following table.
is given in the following table.
|
|
0 |
1 |
2 |
3 |
4 |
5 |
|
|
0.20 |
0.25 |
0.35 |
0.40 |
0.75 |
1.00 |
![]() is given in the table below.
is given in the table below.
|
|
0 |
1 |
2 |
3 |
4 |
5 |
|
|
0.20 |
0.25-0.20=0.05 |
0.35-0.25=0.10 |
0.40-0.35=0.05 |
0.75-0.40=0.35 |
1.00-0.75=0.25 |