If![]() observationsare taken from a normal distribution with mean
observationsare taken from a normal distribution with mean![]() andvariance
andvariance![]() the sample mean
the sample mean![]() followsa normal distribution
followsa normal distribution![]()
In practice however thepopulation variance![]() israrely known and must also be estimated. If the variance
israrely known and must also be estimated. If the variance![]() isestimated as
isestimated as![]() (
(![]() isunbiased for
isunbiased for![]() sothat
sothat![]() )from a large sample of size
)from a large sample of size![]() then,the sample mean is approximately normally distributed,
then,the sample mean is approximately normally distributed,![]() theaccuracy of the approximation improving with increasing
theaccuracy of the approximation improving with increasing![]() until,at
until,at ![]() thet distribution is identical to the normal distribution.
thet distribution is identical to the normal distribution.
When n is small however, thenormal approximation given above is not accurate enough and we mustuse Student's t – distribution:
If a random sample![]() isselected from a normal distribution with mean
isselected from a normal distribution with mean![]() andunknown variance
andunknown variance ![]() the
the![]() hasa
hasa![]() distribution,where
distribution,where![]()
In fact there is not asingle t distribution. There is a whole family, each with anassociated number of degrees of freedom,![]() hencethe label
hencethe label![]() usedabove.
usedabove.
The![]() distributionis an approximation to the normal distribution for each value of
distributionis an approximation to the normal distribution for each value of![]()
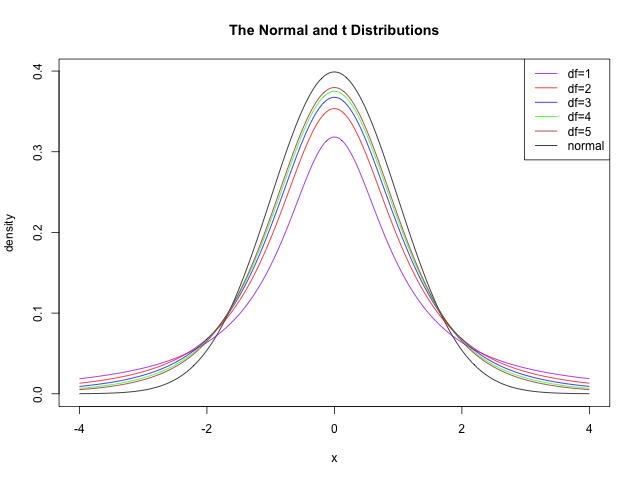
Like the normaldistribution, the t – distribution is symmetrical and unimodal (theprobability density function has one peak, as in the diagram above),and also like the normal distribution, calculations invoving the tdistribution from first principles is not elementary and must be donefrom tables.