Absolute Magnitude
In astronomy, absolute magnitude is the apparent magnitude, ![]() an object would have if it were at a standard distance – 10 parsecs, 32.62 light years or
an object would have if it were at a standard distance – 10 parsecs, 32.62 light years or![]() It allows the overall brightnesses of objects to be compared by compensating for their different distances from us.
It allows the overall brightnesses of objects to be compared by compensating for their different distances from us.
The absolute magnitude uses a log scale. A difference of 1 magnitude corresponds to a factor of 2.512 in intrinsic brightness. A difference of 5 magnitudes corresponds to a factor of![]() in intrinsic brightness.
in intrinsic brightness.
You can compute the absolute magnitude M of a star given its apparent magnitude m and luminosity distance![]() – which is a measure of the ordinary Euclidean distance and is measured in parsecs:
– which is a measure of the ordinary Euclidean distance and is measured in parsecs:
![]()
- For nearby astronomical objects (such as stars in our galaxy) the luminosity distance D Lis almost identical to the real distance to the object, because spacetime within our galaxy is almost Euclidean. For much more distant objects the Euclidean approximation is not valid, and General Relativity must be taken into account when calculating the luminosity distance of an object.
Example: Rigel has apparent visual magnitude
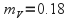 and is at a distance of 773 light years
and is at a distance of 773 light years

The absolute magnitudes of some stars are shown in the table.
Star
Absolute Magnitude
Sun
4.83
Sirius
1.45
Vega
0.58
Spica
-3.55
Barnard;s Star
13.24
Proxima Centauri
15.45
It is important to note that large positive numbers imply dimness and large negative numbers imply brightness.