Lost Energy When Charging and Discharging Capacitors

When a chargemoves through a potential differencethe energy change isIf the voltage is constant, then the energy change is proportional to the charge transferred. However, the voltage is not generally constant. When a capacitor is being charged the voltage is increasing. The equationobeyed by capacitors implies that the voltage is directly proportional to the charge. If we draw a graph of voltage against charge we obtain a straight line graph through the origin.

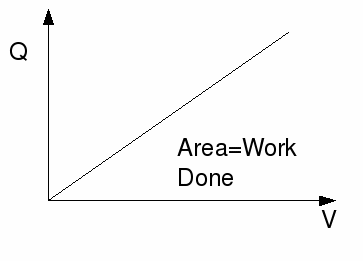
Then the work done in charging the capacitor is equal to the area under the graph is

The energy delivered when a capacitor is being discharged is alsofor the same reasons.

We can show this mathematically. For a charging capacitor at any time, andso the work done in transferring a small amount of chargethrough a potential differenceis

Then

Energyis needed to charge the capacitor but when fully charged the capacitor only storesThe 'missing' energy is used to overcome resistance in the charging circuit.