Navigation 2
When a plane takes off and flies towards it destination it must take account of the wind. If it does not it will be blown off course.Suppose has to fly from a point A to a point B on a bearing of 060 degrees. The wind is blowing at 40 km/h on a bearing of 149 degrees. In still air the plane flies at a speed of 650 km/h. From this information we can draw the vector diagram/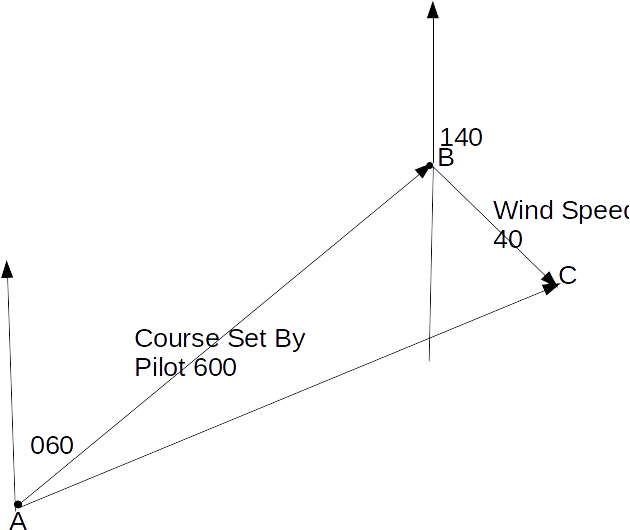

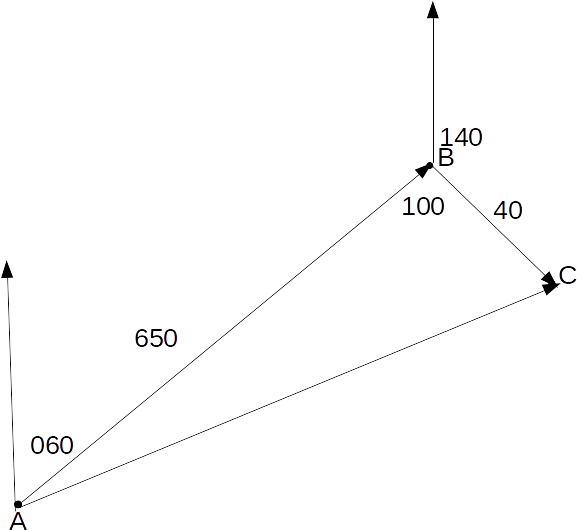
\[AC^2 = AB^2 + BC^2 - 2 \times AB \times BC \times cps B = 650^2 +40^2 -2 \times 650 \times 40 \times cos 100 =433130 \]
\[AC = \sqrt{433139}=658.1\]
The speed of the plane relative to the ground is 658.1 km/h. From the Sine Rule,
\[\frac{BC}{sin A} = \frac{AC}{sin B} \rightarrow sin A = \frac{BC sin B}{AC}=\frac{40 sin 100}{658.1}=0.05986 \rightarrow A = sin^{-1} (0.05986)=3.431\]
degrees.The plane will fly on a course of 063.431 degrees.