Bodies are not rigid and even though the amount of stretching may be small when they are subjected to stretching forces, they often cannot be ignored. The forces involved can be very large, ans must often be taken into account to avoid disaster. For stress and strain up to a certain level, the elastic limit, the stress and strain are proportional.
We may define a ratio,![]()
The Stress is defined as![]()
The Strain is defined as![]()
Hence we may also write![]()
The Young's Modulus of a material is a measure of it's strength. If a material has a high Young's Modulus it is strong and resists stretching. Some values are given in the table below.
|
Material |
Young's Modulus - Pa |
|
Aluminium |
|
|
Iron |
|
|
PTFE |
|
|
Nylon |
|
|
Glass |
|
|
Diamond |
|
We can rearrange the equation (1) into the form![]() and compare it with the equation for the energy stored in a stretch spring
and compare it with the equation for the energy stored in a stretch spring![]() to give the energy stored in a material in terms of the Young's Modulus.
to give the energy stored in a material in terms of the Young's Modulus.
![]()
Plastic and Brittle Materials
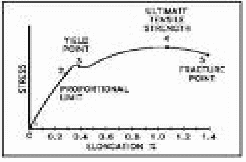
The material in the graph below is elastic. It obeys Hooke's Law up the the elastic limit, then yields..
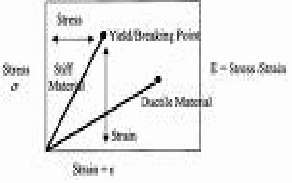
The graph below to the right shows the difference between ductile and brittle. The Young's modulus is the gradient. A larger gradient implies a higher Young's Modulus and a stiffer material. In this case the stiffer material is brittle. It fractures without warning when the stress is greater than the maximum tensile stress it can bear. The ductile material is more like the graph on the left.