The Bohr Model of the Atom
The most important properties of atomic and molecular structure may be illustrated using a simplified picture of an atom, similar to the solar system, called the Bohr Model.
A Planetary Model For The Atom
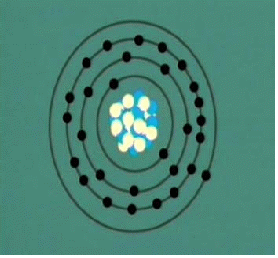
In the Bohr Model the neutrons and protons (symbolized by red and blue balls in the adjacent image) occupy a dense central region called the nucleus, and the electrons orbit the nucleus much like planets orbiting the Sun.
This similarity between a planetary model and the Bohr Model of the atom ultimately arises because the attractive gravitational force in a solar system and the attractive Coulomb (electrical) force between the positively charged nucleus and the negatively charged electrons in an atom are mathematically of the same form - both gravitational and electric forces obey inverse square laws - but the intrinsic strength of the Coulomb interaction is much larger than that of the gravitational interaction; in addition, there are positive and negative electrical charges so the Coulomb interaction can be either attractive or repulsive, but gravitation is always attractive.
Angular Momentum and Energy are Quantized

The basic feature of quantum mechanics that is incorporated in the Bohr Model and that is completely different from the analogous planetary model is that the angular momentum is quantized – it can only come in multiples of a quantity![]() called Planck's constant,
called Planck's constant,![]() This means that only certain orbits are allowed, illustrated above. This leads also to the quantization of energy.
This means that only certain orbits are allowed, illustrated above. This leads also to the quantization of energy.
The adjacent figure shows such quantized energy levels for the hydrogen atom. These levels are labelled by an integer n that is called a quantum number. The lowest energy state is generally termed the ground state. The ground state of hydrogen has energy of -13.6eV. The states with successively more energy than the ground state are called the first excited state, the second excited state, and so on. Beyond an energy called the ionization potential the single electron of the hydrogen atom is no longer bound to the atom. Then the energy levels form a continuum. The energy of each excited state is given by ![]()
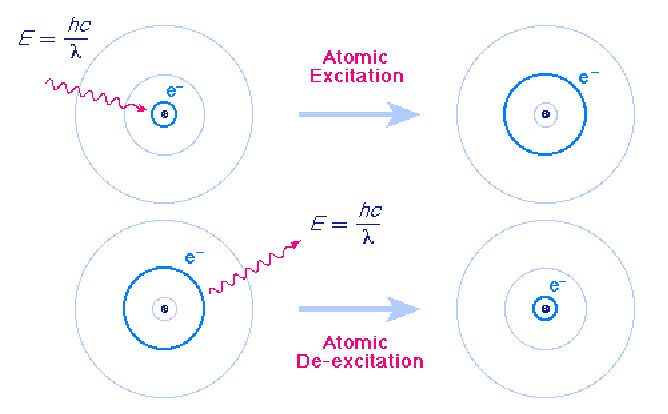
Atomic Excitation and De - excitation
Atoms can make transitions between the orbits allowed by quantum mechanics by absorbing or emitting exactly the energy difference between the orbits. The following figure shows an atomic excitation cause by absorption of a photon and an atomic de-excitation caused by emission of a photon.
In each case the wavelength of the emitted or absorbed light is exactly such that the photon carries the energy difference between the two orbits. This energy us given by the formula