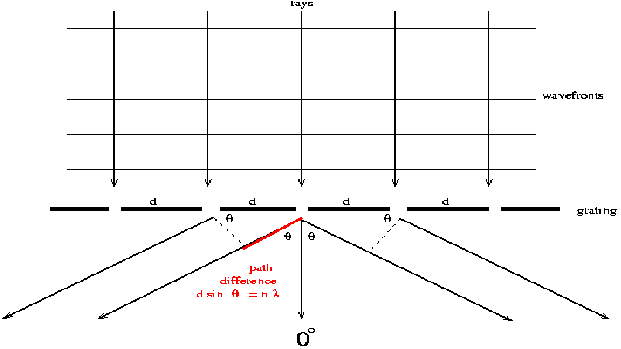
Example: L Light of wavelength![]() is incident on a diffraction grating which has 600000 lines per metre. Find all the angles corresponding to the maxima.
is incident on a diffraction grating which has 600000 lines per metre. Find all the angles corresponding to the maxima.
If there are 600000 lines per m,![]()
![]()
If![]() degrees.
degrees.
If![]() degrees.
degrees.
If![]() degrees
degrees
If![]() degrees.
degrees.
If![]() and this has no solution, so the maximum value for the order is 4. Note that there is one fringe on either side and a bright fringe in the middle so if a diffraction pattern has
and this has no solution, so the maximum value for the order is 4. Note that there is one fringe on either side and a bright fringe in the middle so if a diffraction pattern has![]() orders there are
orders there are![]() fringes.
fringes.