Properties of Simple Harmonic Motion
The general equation of simple harmonic motion is![]() and the general solution to this equation is
and the general solution to this equation is![]() The amplitude of the oscillations is
The amplitude of the oscillations is![]() The constants A and B are arbitrary. In particular, they do not depend on the period of oscillations. This may be surprising, but it is a universal feature of simple harmonic motion that the period and the amplitude are independent of each other. On the other hand, the period does depend on the physical constants of the apparatus, while the amplitude is determined by the initial conditions - how the motion starts.
The constants A and B are arbitrary. In particular, they do not depend on the period of oscillations. This may be surprising, but it is a universal feature of simple harmonic motion that the period and the amplitude are independent of each other. On the other hand, the period does depend on the physical constants of the apparatus, while the amplitude is determined by the initial conditions - how the motion starts.
For instance, the simple pendulum obeys the equation![]() and then
and then![]() and
and![]() the length of the pendulum, is a property of the pendulum.
the length of the pendulum, is a property of the pendulum.
A mass m on a spring with spring constant k obeys the equation ![]() and then
and then![]()
In theory almost any oscillation may be approximated by simple harmonic motion if the oscillation in small enough.
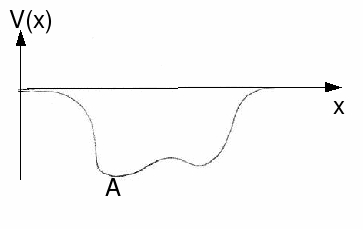
For small oscillations about the point A, the motion may be simple harmonic because the potential for a small interval at A is approximately symmetric and A is a minimum.