Quadratic Inequalities
To solve the inequality\[x^2-4x+3 \gt 0\]
, first factorise to give \[(x-1)(x-3) \gt 0\]
.Now sketch the graph of
\[y=x^2-4x+3\]
.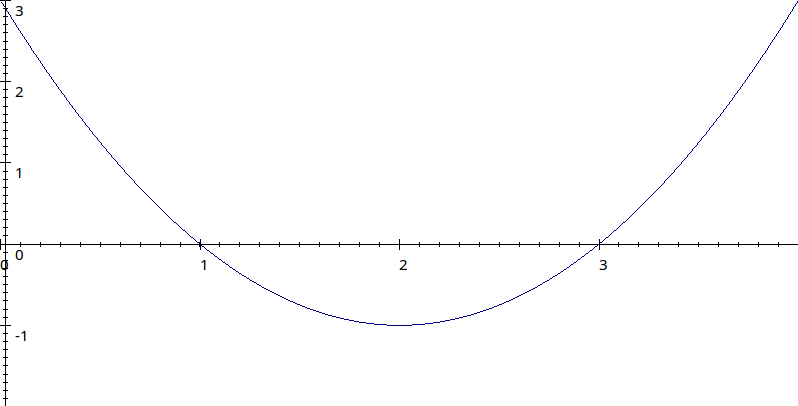
\[x^2-4x+3 \gt 0\]
we want those values of \[y \gt 0\]
.From the graph we see this is true for
\[x \lt 0\]
or \[x \gt 3\]
.For the inequality
\[x^2-4x+3 \lt 0\]
, we need that part of the graph below the \[x\]
axis. The solution is \[1 \lt x \lt 3\]
.To solve the inequality
\[x^2-4x+3 \ge 0\]
, just replace each 'greater than' sign with 'greater than or equal to' and each 'less than' sign with a 'less than or equal to' sign. We get \[x \le 1\]
or \[x \ge 3\]
.