Perimeter of Shape Fomed By Four Circles Equally Spaced About an Inner Circle
The diagram shows four circles equal spaced around another circle, with the centre on each outer circle on the circumference of the centre circle. What is the perimeter of the shape?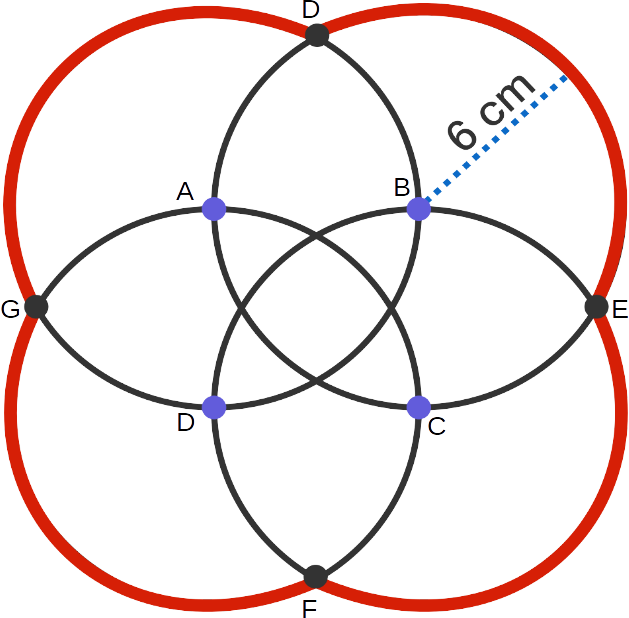
\[360-90-2 \times 60=150\]
degrees.The perimeter of the shape is then
\[4 \times \frac{150}{360} \times 2 \pi \times 6= 20 \pi\]
.