Area of a Regular Polygon in a Circle of Radius r
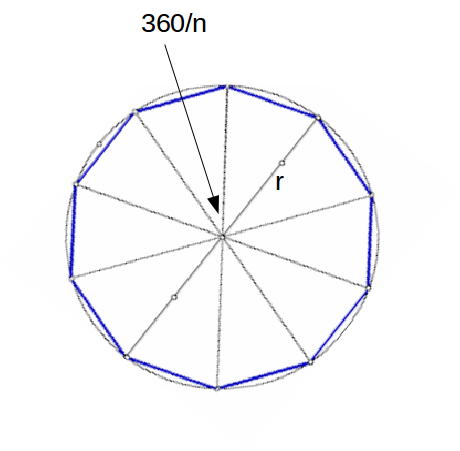
Suppose a regular polygon with\[n\]
sides is inscribed in a circle of radius \[r\]
, with the vertices of the polygon touching the circle.From the centre of the circle lines are drawn to each vertex, and
\[n\]
triangles are formed. The angle of each triangle at the centre of the circle is \[\frac{360}{n}\]
, and the area of each triangle is \[\frac{1}{2}r^2 sin (\frac{360}{n})\]
.
\[n\]
such triangles, so the area of the polygon is \[\frac{n}{2}r^2 sin (\frac{360}{n})\]
.As the number of sides gets larger
\[sin (\frac{360}{n}) \]
tends to \[\frac{2 \pi}{n}\]
, so the area of the polygon tends to \[\frac{n}{2} r^2 \times \frac{2 \pi}{n}= \pi r^2\]
.