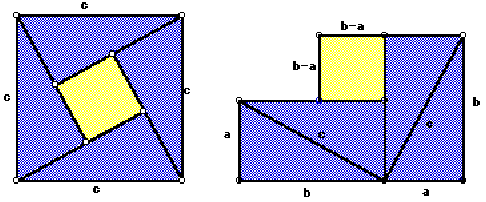
The above diagrams represent rearrangements of sets of shapes.
The blue triangles are all right angled, with the right angles at the corners of the yellow square, and congruent so all have the same area and the yellow squares are congruent so have the same area. We can find the area of the square on the left and equate it to the area of the rearrangement to the right.
The area of the large square on the left is![]()
The area of the shape on the left is![]()
Area of all the blue triangles together![]()
Area of the yellow square![]()
Area of the shape on the right is then![]()
Equating the area of the shape on the left to the area of the shape on the right gives![]()
This is exactly Pythagoras theorem. Note that![]() are the sides of a right angled blue triangle, with c the longest side opposite the right angle.
are the sides of a right angled blue triangle, with c the longest side opposite the right angle.