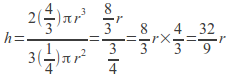If the volumes of two solid is in a certain ratio, we can often find relationships between some lengths of the solids even if the solids are not similar.
Suppose the volume of the cylinder and sphere below are in the ratio 2:3. The radius of the sphere is twice the radius of the cylinder, or equivalently, the radius of the cylinder is half the radius of the sphere. If the radius of the sphere is![]() find the height of the cylinder in terms of
find the height of the cylinder in terms of![]()
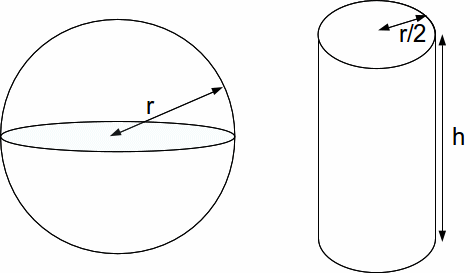
The volume of the sphere is![]()
The volume of a cylinder of radius![]() and height
and height![]() is
is![]() so the volume of the cylinder above is
so the volume of the cylinder above is![]()
The ratio given in the question means that![]() so
so
![]()
Then