A ticker timer is a device that leaves a pencil mark on a piece of paper at regular intervals – typically every 0.02 seconds. If the paper is a strip attached to an accelerating body, the marks made by the tickertape might look like that below.

This might be produced by letting a weight hanging over a pully accelerate a trolly moving on a table as shown in the diagram below.
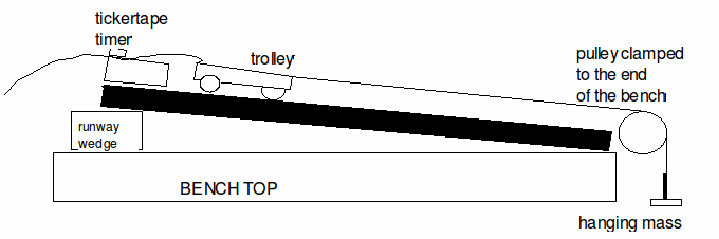
By measuring the distance between each mark on the tape, the average velocity of the particle between marks can be found and hence the acceleration. Typically the distance between more than one mark is taken, to improve accuracy. To check the acceleration is constant, the distance travelled between a certain number of marks can be plotted as below as time progresses. If a line drawn through the midpoints of the bar peaks makes a straight line, then the acceleration is constant.
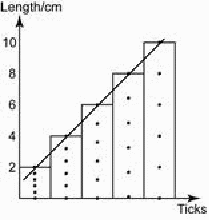
For example 5 ticks in the diagram above are made in the first 2cm of tape and 5 in the last 10 cm (note the first tick only marks the start).
Hence![]() and
and![]()
The time between the first and second strips is taken as![]() This is the time from the middle of the first strip to the middle of the second.
This is the time from the middle of the first strip to the middle of the second.
The acceleration is![]()