Optimising - Maximum Volume From a Rectangular Piece of Card
Suppose we are to make a open topped box out of a rectangular piece of card. We can cut square corners out of the card and fold it up, but what size corners should we cut to maximise the volume of the box?Suppose we cut corners of side
\[x\]
from the card.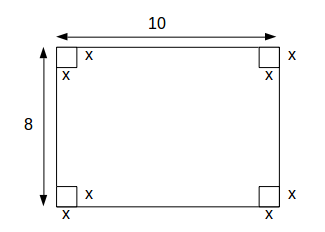
\[x, \: 8-2x, \: 10-2x\]
.The volume is
\[V=x(8-2x)(10-2x)=4x^3-36x^2+80x\]
.To find the maximum volume, start by differentiating.
\[\frac{dV}{dx}=12x^2-72x+80\]
Solve the equation
\[\frac{dV}{dx}=0 \rightarrow 12x^2-72x+80=0 \rightarrow x=\frac{9 \pm \sqrt{21}}{3}\]
.Now differentiate again to find
\[\frac{d^2V}{dx^2}\]
and substitute these values of \[x\]
. If the result is greater than zero, the result is a local minimum for the volume, and if the result is less than zero, the result is a local maximum for the volume.\[\frac{d^2V}{dx^2}=24x-72\]
\[x_1=\frac{9 - \sqrt{21}}{3} \rightarrow \frac{d^2V}{dx^2}=24x_1-72=24(\frac{9 - \sqrt{21}}{3})-72=-8 \sqrt{21} \lt 0 \]
so this returns a maximum volume.\[x_2=\frac{9 + \sqrt{21}}{3} \rightarrow \frac{d^2V}{dx^2}=24x_2-72=24(\frac{9 + \sqrt{21}}{3})-72=8 \sqrt{21} \lt 0 \]
so this returns a minimum volume.The maximum volume is
\[V(x_1)=4(\frac{9 - \sqrt{21}}{3})^3-36(\frac{9 - \sqrt{21}}{3})^2+80(\frac{9 - \sqrt{21}}{3})=\frac{216+56 \sqrt{21}}{9}=52.5 \: units^3\]